点击进群,掌握更多高考升学资讯>>>>高三群 648962469；高二群 102441380；高一群 89582399

查看资讯>>>>升空教育首页   升空讲堂   院校库   专业库

升空教育基于大数据算法推出估分选大学系统，点击此处即可进行测试

1

解决绝对值问题

主要包括化简、求值、方程、不等式、函数等题，基本思路是：把含绝对值的问题转化为不含绝对值的问题。具体转化方法有：

①分类讨论法:根据绝对值符号中的数或式子的正、零、负分情况去掉绝对值。

②零点分段讨论法：适用于含一个字母的多个绝对值的情况。

③两边平方法：适用于两边非负的方程或不等式。

④几何意义法：适用于有明显几何意义的情况。

2

因式分解

根据项数选择方法和按照一般步骤是顺利进行因式分解的重要技巧。因式分解的一般步骤是：

提取公因式

选择用公式

十字相乘法

分组分解法

拆项添项法

3

配方法

利用完全平方公式把一个式子或部分化为完全平方式就是配方法，它是数学中的重要方法和技巧。配方法的主要根据有：

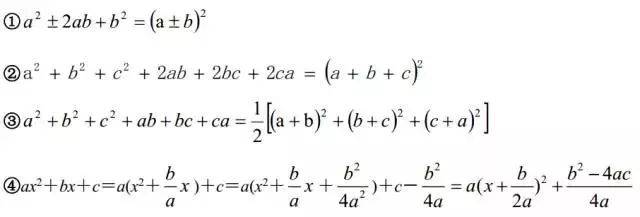
4

换元法

解某些复杂的特型方程要用到“换元法”。换元法解方程的一般步骤是：

设元→换元→解元→还元

5

待定系数法

待定系数法是在已知对象形式的条件下求对象的一种方法。适用于求点的坐标、函数解析式、曲线方程等重要问题的解决。其解题步骤是：

①设 ②列 ③解 ④写

6

复杂代数等式

复杂代数等式型条件的使用技巧：左边化零，右边变形。

①因式分解型：

(-----)(----)=0 两种情况为或型

②配成平方型：

(----)2+(----)2=0 两种情况为且型

7

数学中两个最伟大的解题思路

(1)求值的思路列欲求值字母的方程或方程组

(2)求取值范围的思路列欲求范围字母的不等式或不等式组

8

化简二次根式

基本思路是：把√m化成完全平方式。即：

9

观察法

10

代数式求值

方法有：

(1)直接代入法

(2)化简代入法

(3)适当变形法（和积代入法）

注意：当求值的代数式是字母的“对称式”时，通常可以化为字母“和与积”的形式，从而用“和积代入法”求值。

11

解含参方程

方程中除过未知数以外，含有的其它字母叫参数，这种方程叫含参方程。解含参方程一般要用‘分类讨论法’，其原则是：

(1)按照类型求解

(2)根据需要讨论

(3)分类写出结论

12

恒相等成立的有用条件

(1)ax+b=0对于任意x都成立关于x的方程ax+b=0有无数个解a=0且b=0。

(2)ax2＋bx＋c＝0对于任意x都成立关于x的方程ax2＋bx＋c＝0有无数解a=0、b=0、c=0。

13

恒不等成立的条件

由一元二次不等式解集为R的有关结论容易得到下列恒不等成立的条件：

14

平移规律

图像的平移规律是研究复杂函数的重要方法。平移规律是：

15

图像法

讨论函数性质的重要方法是图像法——看图像、得性质。

定义域 图像在X轴上对应的部分

值 域 图像在Y轴上对应的部分

单调性

从左向右看，连续上升的一段在X轴上对应的区间是增区间；从左向右看，连续下降的一段在X轴上对应的区间是减区间。

最 值 图像最高点处有最大值，图像最低点处有最小值

奇偶性 关于Y轴对称是偶函数，关于原点对称是奇函数

16

函数、方程、不等式简的重要关系

方程的根

函数图像与x轴交点横坐标

不等式解集端点

17

一元二次方程的解法

一元二次不等式可以用因式分解转化为二元一次不等式组去解，但比较复杂；它的简便的实用解法是根据“三个二次”间的关系，利用二次函数的图像去解。具体步骤如下：

二次化为正

判别且求根

画出示意图

解集横轴中

18

一元二次方程根的讨论

一元二次方程根的符号问题或m型问题可以利用根的判别式和根与系数的关系来解决，但根的一般问题、特别是区间根的问题要根据“三个二次”间的关系，利用二次函数的图像来解决。“图像法”解决一元二次方程根的问题的一般思路是：

题意

二次函数图像

不等式组

不等式组包括：a的符号；△的情况；对称轴的位置；区间端点函数值的符号。

19

基本函数在区间上的值域

我们学过的一次函数、反比例函数、二次函数等有名称的函数是基本函数。基本函数求值域或最值有两种情况：

(1)定义域没有特别限制时---记忆法或结论法；

(2)定义域有特别限制时---图像截断法，一般思路是：

画出图像

截出一断

得出结论

20

最值型应用题的解法

应用题中，涉及“一个变量取什么值时另一个变量取得最大值或最小值”的问题是最值型应用题。解决最值型应用题的基本思路是函数思想法，其解题步骤是：

设变量

列函数

求最值

写结论

21

穿线法

穿线法是解高次不等式和分式不等式的最好方法。其一般思路是：

首项化正

求根标根

右上起穿

奇穿偶回

注意：①高次不等式首先要用移项和因式分解的方法化为“左边乘积、右边是零”的形式。②分式不等式一般不能用两边都乘去分母的方法来解，要通过移项、通分合并、因式分解的方法化为“商零式”，用穿线法解。

文章整理自网络，如有侵权请联系管理员删除